Overview
Entropy is a notoriously tricky concept. It’s associated with many ideas: disorder, randomness, messiness, uncertainty, information, energy and the arrow of time to name a few. To complicate matters, the notion of entropy originated from different fields: thermodynamics and statistical mechanics (which are both branches of physics) and later, information theory (which is a branch of mathematics and computer science).
In this post we’ll explore the evolution and generalisation of the concept of entropy, see how it relates to both physics and information, discuss paradoxes, demons, black holes and the end of the universe.
Prior to research for this post, I understood entropy at a surface level having used it in a machine learning context and reading about it in popular science books. This is my attempt to understand entropy in its various forms at a deeper level.

What is Entropy?
Entropy is basically a measure of randomness. If your room is tidy and organised, you can say it has a low entropy arrangement. However, if your room is a mess with things everywhere randomly, you can say it has a high entropy arrangement. In some sense, entropy is related to the number of ways objects can be arranged: there are many more ways for a room to be messy compared to organised. This imbalance between messy vs. organised states is at the heart of entropy and leads to very interesting results for any system, including your room or even the entire universe!
Wikipedia describes entropy as: “a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognised, to the microscopic description of nature in statistical physics, and to the principles of information theory.”
The use of the term entropy in multiple fields is one reason it can be a confusing concept as it is defined and interpreted somewhat different is each. Let’s review the three main fields it’s used:
Thermodynamics is a branch of physics that deals with the relationships between heat, energy, and temperature. It is fundamental to understanding the behaviour of a physical system, such as an engine. In classical thermodynamics, entropy is a quantitative, measurable, macroscopic physical property invented to describe heat transfer in systems. Famously, the second law of thermodynamics says that all processes in a system have a direction, from lower to higher entropy, which reduces the amount of useable energy available. The unusable energy takes the form of heat. This asymmetry within a system can be used empirically to distinguish past and future and establishes entropy as an arrow of time.
Statistical mechanics (also known as statistical thermodynamics) is considered the third pillar of modern physics, next to quantum theory and relativity theory. It emerged with the development of atomic theories, explaining classical macroscopic thermodynamics as a result of statistical methods applied to large numbers of microscopic entities. In statistical mechanics, entropy is a measure of the number of ways a system can be arranged. Less likely “ordered” arrangements having low entropy, and more likely “unordered” arrangements having high entropy.
Information theory is a mathematical approach to studying the coding of information for storage and transmission. Information entropy is analogous to statistical mechanics entropy, while being a more general concept. In information theory, entropy is the average level of “information content” or “surprise” of observed outcomes from a random process. For example, flipping a coin 10 times and observing 10 heads is more surprising (and so has higher entropy) than observing a mix of heads and tails, which is less surprising. Another interpretation of information entropy is the amount of information (measured in bits) needed to fully describe a system.
So entropy has different formulations, and varying interpretations, depending the field it’s used in. Even within a single field entropy can be defined in different ways, as we will see later. However, over time it’s been shown that all formulations are related.
While the concept of entropy may seem abstract, it has many real world applications across physics, chemistry, biological systems, economics, climate change, telecommunications and even the big bang and the arrow of time!
Deeper Dive into the Different Guises of Entropy
The following sections take a deeper dive into the concept of entropy in the fields described above.
1. Classical Thermodynamic Entropy in Physics (Carnot & Clausius)
In 1865, Rudolf Clausius (1822 - 1888) gave irreversible heat loss a name: Entropy. He was building on the work of Carnot (1796 - 1832) who laid the foundations of the discipline of thermodynamics while looking to improve the performance of steam engines. Classical thermodynamics is the description of systems near-equilibrium using macroscopic, measurable properties. It models exchanges of energy, work and heat based on the laws of thermodynamics. The qualifier classical reflects the fact that it represents the first level of understanding of the subject as it developed in the 19th century and describes the changes of a system in terms of macroscopic parameters.
There are 4 laws of thermodynamics. The second law establishes the concept of entropy as a physical property of a thermodynamic system and states that if a physical process is irreversible, the combined entropy of the system and the environment must increase. Importantly this implies that a perpetual motion machine is physically impossible. For a reversible process which is free of dissipative losses, total entropy may be conserved, however such physical systems cannot exist. The Carnot cycle is an idealised reversible process that provides a theoretical upper limit on the efficiency of any classical thermodynamic engine.
The 1865 paper where Clausius introduced the concept of entropy ends with the following summary of the first and second laws of thermodynamics:
The energy of the universe is constant.
The entropy of the universe tends to a maximum.
Clausius also gives the expression for the entropy production for a cyclical process in a closed system, which he denotes by N. Here Q is the quantity of heat, T is the temperature, S is the final state entropy and S0 the initial state entropy. S0 - S is the entropy difference for the backwards part of the process. The integral is to be taken from the initial state to the final state, giving the entropy difference for the forwards part of the process. From the context, it is clear that N = 0 if the process is reversible and N > 0 in case of an irreversible process.

Next we shift gears from the macroscopic to the microscopic realm…
2. Statistical Mechanics Entropy in Physics (Gibbs & Boltzmann)
Statistical mechanics, also known as statistical thermodynamics, emerged with the development of atomic and molecular theories in the late 19th century and early 20th century. It supplemented classical thermodynamics with an interpretation of the microscopic interactions between individual particles and relates the microscopic properties of individual atoms to the macroscopic, bulk properties of materials that can be observed on the human scale, thereby explaining classical thermodynamics as a natural result of statistics and classical mechanics. It is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. It does not assume or postulate any natural laws, but explains the macroscopic behaviour of nature from the behaviour of such ensembles.
Josiah Willard Gibbs (1839 - 1903) coined the term statistical mechanics which explains the laws of thermodynamics as consequences of the statistical properties of the possible states of a physical system which is composed of many particles. In Elementary Principles in Statistical Mechanics (1902), which is considered to be the foundation of modern statistical mechanics, he writes:
Although, as a matter of history, statistical mechanics owes its origin
to investigations in thermodynamics, it seems eminently worthy of an
independent development, both on account of the elegance and simplicity
of its principles, and because it yields new results and places old truths
in a new light. - Gibbs
Ludwig Boltzmann (1844 - 1906) is the other leading figure of statistical mechanics and developed the statistical explanation of the second law of thermodynamics. In 1877 he provided what is known as the Boltzmann definition of entropy, S:
where Ω is the number of distinct microscopic states available to the system given a fixed total energy, and kB the Boltzmann constant. The Boltzmann constant, and therefore Boltzmann entropy, have dimensions of energy divided by temperature, which has a unit of joules per kelvin (J⋅K−1) or kg⋅m2⋅s−2⋅K−1 in terms of base units. It could have been chosen to have any value, including 1 (i.e. dimensionless), however for historical reasons it was chosen to have the value: kB = 1.38649 × 10−23 joules per kelvin. As described by danielsank, kB only exists because people defined temperature and entropy before they understood statistical mechanics. If temperature had dimensions of energy, then under this definition entropy would have been dimensionless.
Gibbs refined this formulation and generalised Boltzmann's statistical interpretation of entropy in his work Elementary Principles in Statistical Mechanics (1902) by defining the entropy of an arbitrary ensemble as:
where kB is the Boltzmann constant, while the sum is over all possible microstates i, with pi the corresponding probability of the microstate. Both Boltzmann and Gibbs entropies are the pillars of the foundation of statistical mechanics and are the basis of all the entropy concepts in modern physics.
As described by ACuriousMind, the Gibbs entropy is the generalisation of the Boltzmann entropy holding for all systems, while the Boltzmann entropy is only the entropy if the system is in global thermodynamical equilibrium (when there is no net macroscopic flows of matter or energy within the system). Both are a measure for the microstates available to a system, but the Gibbs entropy does not require the system to be in a single, well-defined macrostate.
The second law of thermodynamics states that the total entropy of an isolated system always increases over time. It is a statistical law rather than an absolute law. The statistical nature arises from the fact that it is based on the probability of different configurations of the particles in a system, and how those probabilities change over time. It is not impossible, in principle, for all atoms in a box of a gas to spontaneously migrate to one half; it is only astronomically unlikely.
Entropy is one of the few quantities in the physical sciences that require a particular direction for time and provides a natural explanation for why we observe an arrow of time in the universe. It explains why systems tend to become more disordered over time, and why we perceive time as having a certain direction from past to future. In cosmology, the past hypothesis postulates that the universe started in a low-entropy state which was highly ordered and uniform and this is responsible for the observed structure and organisation of the universe today which is compatible with the second law. At the other end of the spectrum, the heat death of the universe is a hypothesis on the fate of the universe stating the universe will evolve to a state of no thermodynamic free energy, and will therefore be unable to sustain processes that increase entropy. Luckily this should take over 10^100 years. It is suggested that, over vast periods of time, a spontaneous entropy decrease would eventually occur creating anther universe, but in reality we have no idea. To wrap up the cosmological angle, it’s interesting to note that a black hole has an entropy that is proportional to its surface area, rather than its volume, implying that the entropy increases as it absorbs more matter.
The Gibbs paradox is a thought experiment puzzle in statistical mechanics that arises from the different ways of counting the number of possible arrangements of particles in a mixture of two identical gases within a box. One way is to assume that particles are distinguishable, while the other assumes they are indistinguishable. These two ways of counting can lead to different predictions for the entropy of the system, and result in a paradox if we are not careful to specify particle distinguishability. The paradox is resolved when we realise that we need to take into account the fact that identical particles can be swapped with each other without changing the overall arrangement. When we do this, we find that the number of possible arrangements for two identical gases is actually greater than the number of possible arrangements for two different gases. This explains why the entropy of a mixture of identical gases is higher than the entropy of a mixture of different gases.
Next we shift gears again, from the physical world to the informational world…
3. Information and Communication Entropy (Shannon)
Information theory is the scientific study of the quantification, storage, and communication of information. In 1948, Claude Shannon set out to mathematically quantify the statistical nature of “lost information” in phone-line signals. To do this, Shannon developed the very general concept of information entropy which was published in his A Mathematical Theory of Communication. Shannon considered various ways to encode, compress, and transmit messages, and proved that the entropy represents an absolute mathematical limit on how well data from a source can be losslessly compressed onto a perfectly noiseless channel.

The core idea of information theory is that the “informational value” of a message depends on the degree to which the content of the message is surprising. If a highly likely event occurs, the message carries very little information. However, if a highly unlikely event occurs, the message is much more informative. Information theory often concerns itself with measures of information of the distributions associated with random variables. The entropy of a random variable is the average level of “information”, “surprise”, or “uncertainty” inherent to the variable's possible outcomes.
Shannon entropy, H, can be defined as:
where p(x) is the probability of outcome x and b is the logarithm base, where b = 2 encodes binary digits.

Shannon entropy is clearly analogous to Gibbs entropy, without the Boltzmann constant. The analogy results when the values of the random variable designate energies of microstates. In the view of Jaynes, entropy within statistical mechanics should be seen as an application of Shannon's information theory: the thermodynamic entropy is interpreted as being proportional to the amount of further Shannon information needed to define the detailed microscopic state of the system, that remains uncommunicated by a description solely in terms of the macroscopic variables of classical thermodynamics. For example, adding heat to a system increases its thermodynamic entropy because it increases the number of possible microscopic states of the system that are consistent with the measurable values of its macroscopic variables, making any complete state description longer.
Maxwell's demon is a thought experiment, proposed in 1867, that would hypothetically violate the second law of thermodynamics. In the experiment a demon controls a door between two chambers of gas. As gas molecules approach the door, the demon allows only fast-moving molecules through in one direction, and slow-moving in the other direction, causing one chamber to warm up and the other to cool down. This decreases the total entropy of the system, without applying any work, hence the violation. It stimulated work on the relationship between thermodynamics and information theory.

Maxwell's demon can (hypothetically) reduce the thermodynamic entropy of a system by using information about the states of individual molecules; but, as Landauer showed in 1961, to function the demon himself must increase thermodynamic entropy in the process, by at least the amount of Shannon information he proposes to first acquire and store; and so the total thermodynamic entropy does not decrease (which resolves the paradox). Landauer's principle is a physical principle pertaining to the lower theoretical limit of energy consumption of computation. It imposes a lower bound on the amount of heat a computer must generate to process a given amount of information, though modern computers are far less efficient.
The principle of maximum entropy states that the probability distribution which best represents the current state of knowledge about a system is the one with largest entropy, in the context of precisely stated prior data. The principle was first expounded by Jaynes where he emphasised a natural correspondence between statistical mechanics and information theory. It can be said to express a claim of maximum ignorance. The selected distribution is the one that makes the least claim to being informed beyond the stated prior data, that is to say the one that admits the most ignorance beyond the stated prior data.
The principle of maximum entropy is commonly applied to inferential problems, for example, to obtain prior probability distributions for Bayesian inference or making predictions with logistic regression, which corresponds to the maximum entropy classifier for independent observations. Giffin and Caticha (2007) state that Bayes' theorem and the principle of maximum entropy are completely compatible and can be seen as special cases of the “method of maximum relative entropy”. Jaynes stated, in 1988, that Bayes' theorem was a way to calculate a probability, while maximum entropy was a way to assign a prior probability distribution.
A Review of Different Entropy Measures
We’ve touched upon the key measures of entropy as the concept matured and generalised since around 1865. There are many additional definitions that are related to each other in different ways.
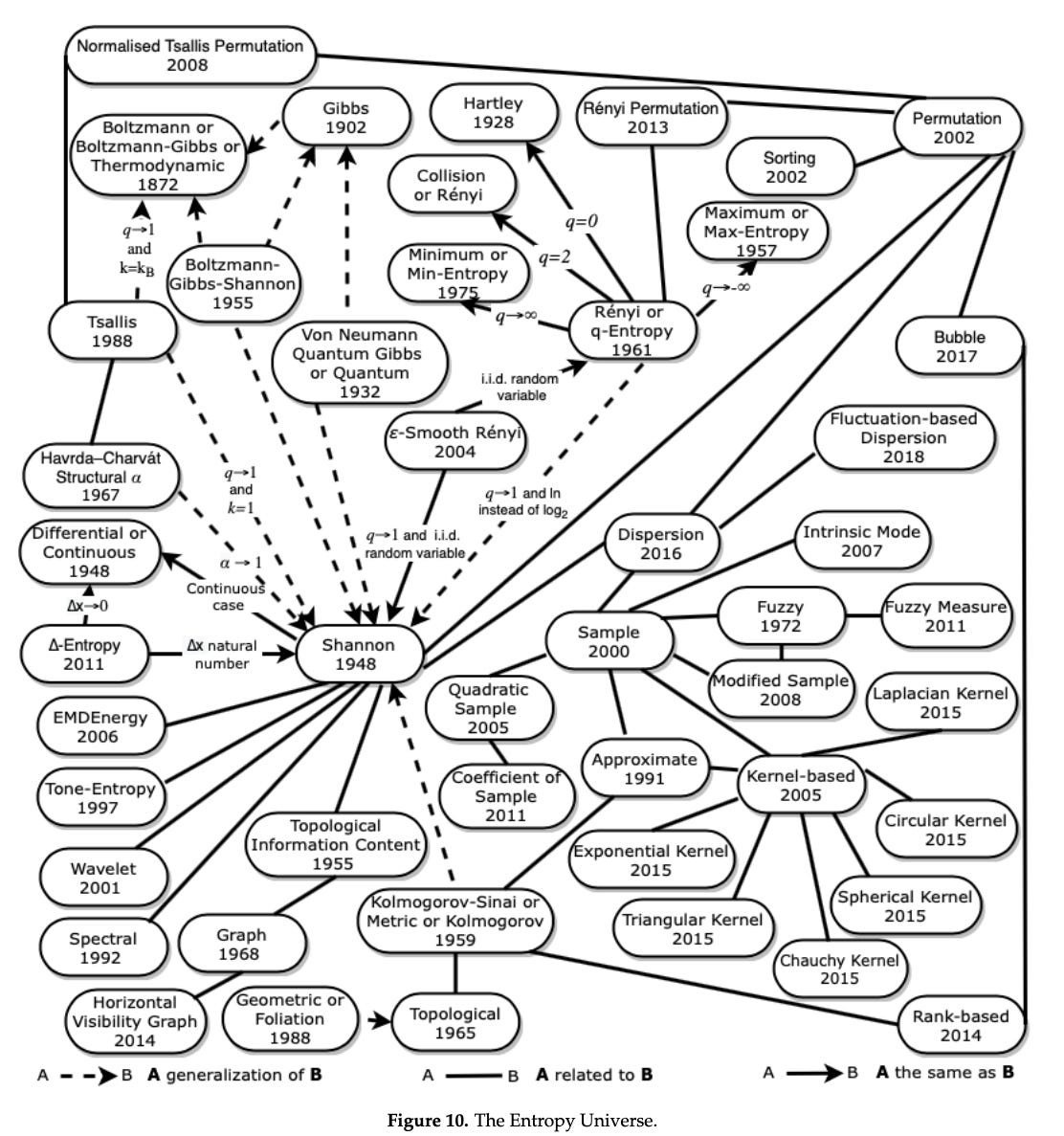
The Entropy Universe (2021) by Ribeiro et al, is a paper which aims to review the many variants of entropy definitions and how they relate to each other. The authors describe the relationship between the most applied entropies for different scientific fields, establishing bases for researchers to properly choose the variant of entropy most suitable for their data. It’s well worth checking out.
For example, here is the timeline (in logarithmic scale) of the universe of entropies covered in the paper:

And here is the full entropy relation diagram, which can be found on page 21:
The People Behind Entropy
It’s helpful to understand the timeline over which concept of entropy has evolved, from 19th century combustion engines to modern communications.
In the 19th century people were building combustion engines and observed that some energy released from combustion reactions was always lost and not transformed into useful work. Investigations into trying to solve this problem led to the initial concept of entropy.
Nicolas Léonard Sadi Carnot (1796 - 1832; thermodynamics)
Carnot was a French mechanical engineer and the “father of thermodynamics”. His work was used by Clausius and Kelvin to formalise the second law of thermodynamics and define the concept of entropy.
Rudolf Clausius (1822 - 1888; thermodynamics)

In 1865 Clausius, a German physicist, introduced and named the concept of entropy. He studied the mechanical theory of heat and built upon Carnot’s work. His most important paper, “On the Moving Force of Heat” first stated the basic ideas of the second law of thermodynamics.
William Thomson (Lord Kelvin) (1824 - 1907; thermodynamics)
Kelvin did important work in the mathematics of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging discipline of physics in its contemporary form. He also coined term thermodynamics in his publication “An Account of Carnot's Theory of the Motive Power of Heat”.
James Clerk Maxwell (1831 - 1879; statistical mechanics)
Maxwell, was a Scottish mathematician and scientist, helped develop the Maxwell–Boltzmann distribution - a statistical means of describing aspects of the kinetic theory of gases. Also proposed “Maxwell's demon” a paradoxical thought experiment where entropy decreases.
Ludwig Boltzmann (1844 - 1906; statistical mechanics)

Boltzmann, an Austrian physicist and philosopher, developed the statistical explanation of the second law of thermodynamics. He also developed the fundamental statistical interpretation of entropy (Boltzmann entropy) in terms of a collection of microstates.
Josiah Willard Gibbs - Wikipedia (1839 - 1903; statistical mechanics)

Gibbs, an American scientist, generalised Boltzmann's entropy, so that a system could exchange energy with its surroundings (Gibbs entropy). He also coined the term statistical mechanics which explains the laws of thermodynamics as consequences of the statistical properties of the possible states of a physical system which is composed of many particles. His papers from the 1870s introduced the idea of expressing the internal energy of a system in terms of the entropy, in addition to the usual state-variables of volume, pressure, and temperature.
John von Neumann (1903 - 1957)
In physics, the von Neumann entropy, named after John von Neumann, is an extension of the concept of Gibbs entropy from classical statistical mechanics to quantum statistical mechanics.
Claude Shannon (1916 - 2001)

Known as a "father of information theory". Shannon developed information entropy as a measure of the information content in a message, which is a measure of uncertainty reduced by the message. In so doing, he essentially invented the field of information theory.
Edwin Thompson Jaynes (1922 - 1998)
Wrote extensively on statistical mechanics and on foundations of probability and statistical inference, initiating in 1957 the maximum entropy interpretation of thermodynamics.
Final Thoughts
As stated in the introduction, entropy is a notoriously tricky concept associated with many concepts, and we’ve only scratched the surface on this fascinating concept here.
I’ve certainly enjoyed researching for this post and apologies if it’s a bit rough, but it’s time to click publish and get it out as it’s been sitting in draft for a while.
I hope to write another related post, particularly expanding on Shannon information entropy, quantities of information, complexity, randomness, quantum information and how they’re all related.
Selected Resources
I’ll wrap up with links to resources I found valuable reading. Thanks for reading this far, I hope you got something out of it!
Entropic Physics: Probability, Entropy, and the Foundations of Physics (Caticha, 2022)
Entropy, Information, and the Updating of Probabilities (Caticha, 2021)
Lectures on Probability, Entropy, and Statistical Physics (Ariel Caticha, 2008)
The Entropy Universe - a timeline of entropies (Ribeiro et al, 2021)
Researchers in an Entropy Wonderland - A Review of the Entropy Concept (Popovic, 2017)
A Mathematical Theory of Communication (Shannon, 1948)
Information Theory and Statistical Mechanics (Jaynes, 1957)
Information Theory and Statistical Mechanics II (Jaynes, 1957)
Information Theory and Statistical Mechanics - Lecture Notes (Jaynes, 1962)
Where do we Stand on Maximum Entropy (Jaynes, 1978)
The Relation of Bayesian and Maximum Entropy Methods (Jaynes, 1988)
Irreversibility and heat generation in the computing process (Landauer, 1961)
Is There a Unique Physical Entropy? Micro versus Macro (Dieks, 2012)
Entropy? Exercices de Style (Gaudenzi, 2019)
Quantifying the Rise and Fall of Complexity in Closed Systems (Carroll and Aaronson, 2014)
This post was originally published at blog.infocruncher.com/2023/03/28/entropy-introduction







